Choropleth map

Learn how to create a basic cloropleth map of Spanish population using {ggplot2}
R
spatial
ggplot2
Author

Adrián Cidre

Published

September 30, 2023

1 Description

In this exercise, we will create two choropleth maps using ggplot2:

  • Map of Spanish population by municipality

  • Map of men/women ratio in Spain by municipality

2 Watch the video

3 Load packages

We will use the following packages:

# install.packages("pacman")
library(pacman)

p_load(
  ## Core
  tidyverse,
  
  ## Spatial data manipulation
  sf,
  
  ## Download data
  mapSpain, rnaturalearth,
  
  ## Visualization
  RColorBrewer, ggspatial
)

# High resolution world map
remotes::install_github("ropensci/rnaturalearthhires")

First, I use pacman to load all the packages. Then, I use the tidyverse as the core package for data manipulation and visualization. The package sf will be used to treat the vectorial data. The package mapSpain provide functions to download the administrative boundaries of Spain (click here for further information). The rnaturalearth is a package that will provide us with the world map. However, for using the high resolution map we need also to install {rnturalearthhires} from GitHub. Finally, I will use the {RColorBrewer} package for colour palettes, and the ggspatial to add the map scale and north arrow. So, let’s dive into the exercise!

4 Prepare the data

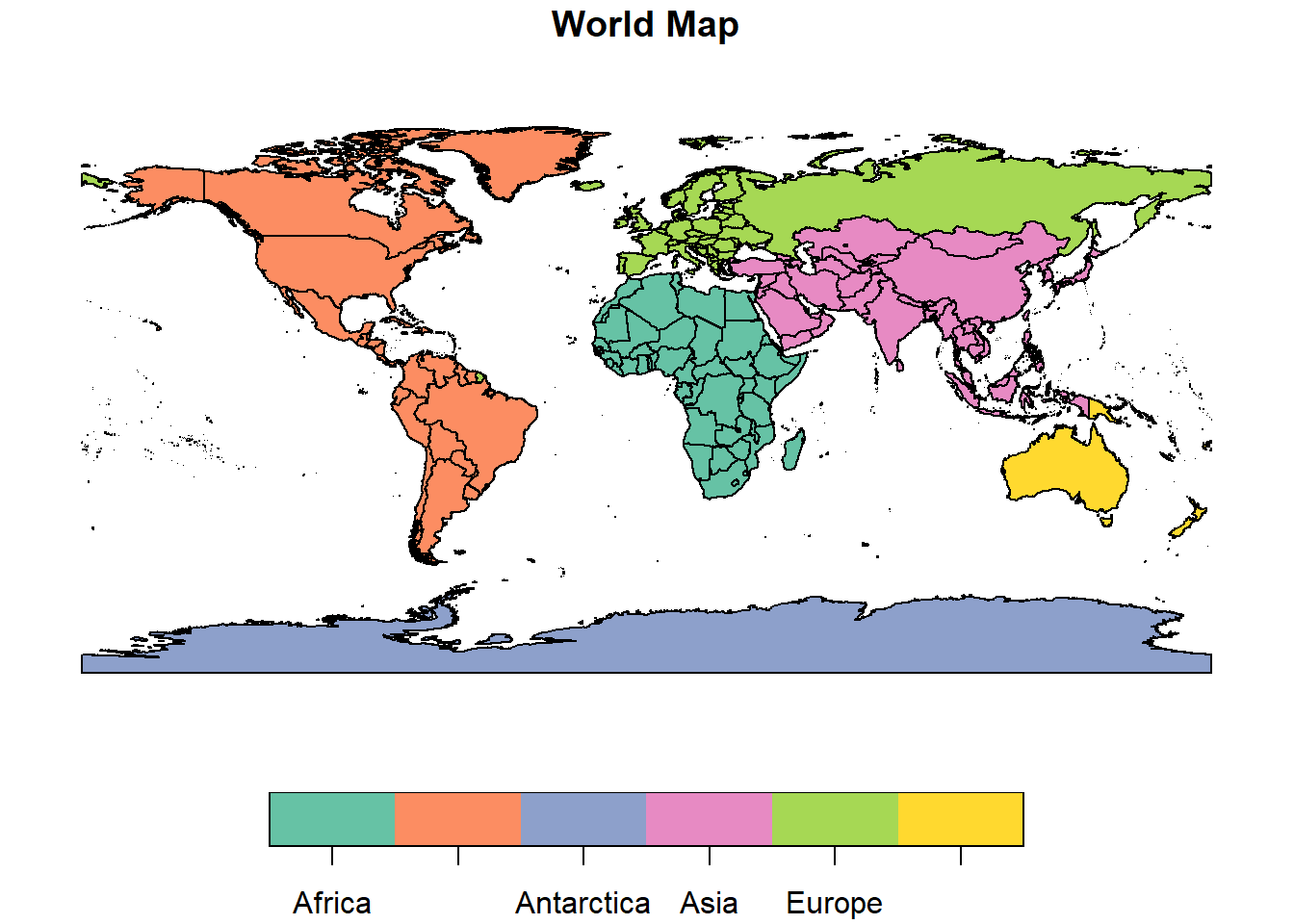
The first step, is to download the world countries map using the ne_countries() function. This will return the map we see in Figure 1.

# World countries
world_sf <- ne_countries(
  scale       = 10,
  returnclass = "sf"
)
plot(world_sf["region_un"], main = "World Map")
Figure 1: World map

Next, we can get the Spanish population by municipality in 2019 using the mapSpain package:

# Get Spanish population by municipality in 2019
spain_pop_tbl <- mapSpain::pobmun19

head(spain_pop_tbl)
  cpro provincia cmun      name  pob19   men women
1   02  Albacete  001 Abengibre    790   379   411
2   02  Albacete  002    Alatoz    519   291   228
3   02  Albacete  003  Albacete 173329 84687 88642
4   02  Albacete  004  Albatana    692   356   336
5   02  Albacete  005   Alborea    658   337   321
6   02  Albacete  006  Alcadozo    654   363   291

This is a data frame with the data we want to plot. However, we need to assign this data to a spatial object with the municipalities. We can get the sf object using the function esp_get_munic:

# Get Spain boundaries by municipality
spain_sf <- esp_get_munic()

head(spain_sf)
Simple feature collection with 6 features and 7 fields
Geometry type: POLYGON
Dimension:     XY
Bounding box:  xmin: -3.14019 ymin: 36.73845 xmax: -2.05701 ymax: 37.54576
Geodetic CRS:  ETRS89
    codauto ine.ccaa.name cpro ine.prov.name cmun      name LAU_CODE
382      01     Andalucía   04       Almería  001      Abla    04001
379      01     Andalucía   04       Almería  002  Abrucena    04002
374      01     Andalucía   04       Almería  003      Adra    04003
375      01     Andalucía   04       Almería  004 Albánchez    04004
358      01     Andalucía   04       Almería  005 Alboloduy    04005
373      01     Andalucía   04       Almería  006     Albox    04006
                          geometry
382 POLYGON ((-2.77744 37.23836...
379 POLYGON ((-2.88984 37.09213...
374 POLYGON ((-2.93161 36.75079...
375 POLYGON ((-2.13138 37.29959...
358 POLYGON ((-2.70077 37.09674...
373 POLYGON ((-2.15335 37.54576...

We see that the data frame spain_pop_tbl and the sf spain_sf share 3 variables:

  • cpro: province code

  • cmun: municipality code

  • name: name of the municipality

The next step is to join both tables together, so we have the data frame attributes in our spatial object. We can achieve this as follows:

# Join population to sf object
spain_pop_sf <- right_join(
  spain_sf,
  spain_pop_tbl,
  by = join_by(cpro, cmun)
)

Note that here I did not include the variable name for joining the dataset. There are two reasons:

  1. The name and cmun variables express exactly the same.
  2. The variable name have some misspellings between datasets creating some NA values.

Once this is clarified, we can begin with the maps.

5 Spanish population

We could plot the Spanish population as a continuous variable, however, this would not be the best approach since the distribution of the population is quite irregular, and there is a small number of cities with very high population. Therefore, we can create bins based on the quantiles:

# Define the breaks (bin edges) based on percentiles
breaks <- quantile(
  spain_pop_sf$pob19, 
  probs = seq(0, 1, by = 0.1)
)

# Round to hundred, and keep unique values
breaks <- round(breaks, -2) %>% unique()
breaks[length(breaks)] <- breaks[length(breaks)] + 100

# Create bins
spain_pop_ready_sf <- spain_pop_sf %>% 
  mutate(
    pop_bin = cut(pob19, breaks = breaks, dig.lab = 10)
  )

print(levels(spain_pop_ready_sf$pop_bin))
[1] "(0,100]"        "(100,200]"      "(200,300]"      "(300,500]"     
[5] "(500,900]"      "(900,1700]"     "(1700,3500]"    "(3500,9200]"   
[9] "(9200,3266200]"

With the previous code we create the new variable called pop_bin which consists in a total of 9 bins representing similar amount of municipalities. Finally, we can represent it graphically with the next code:

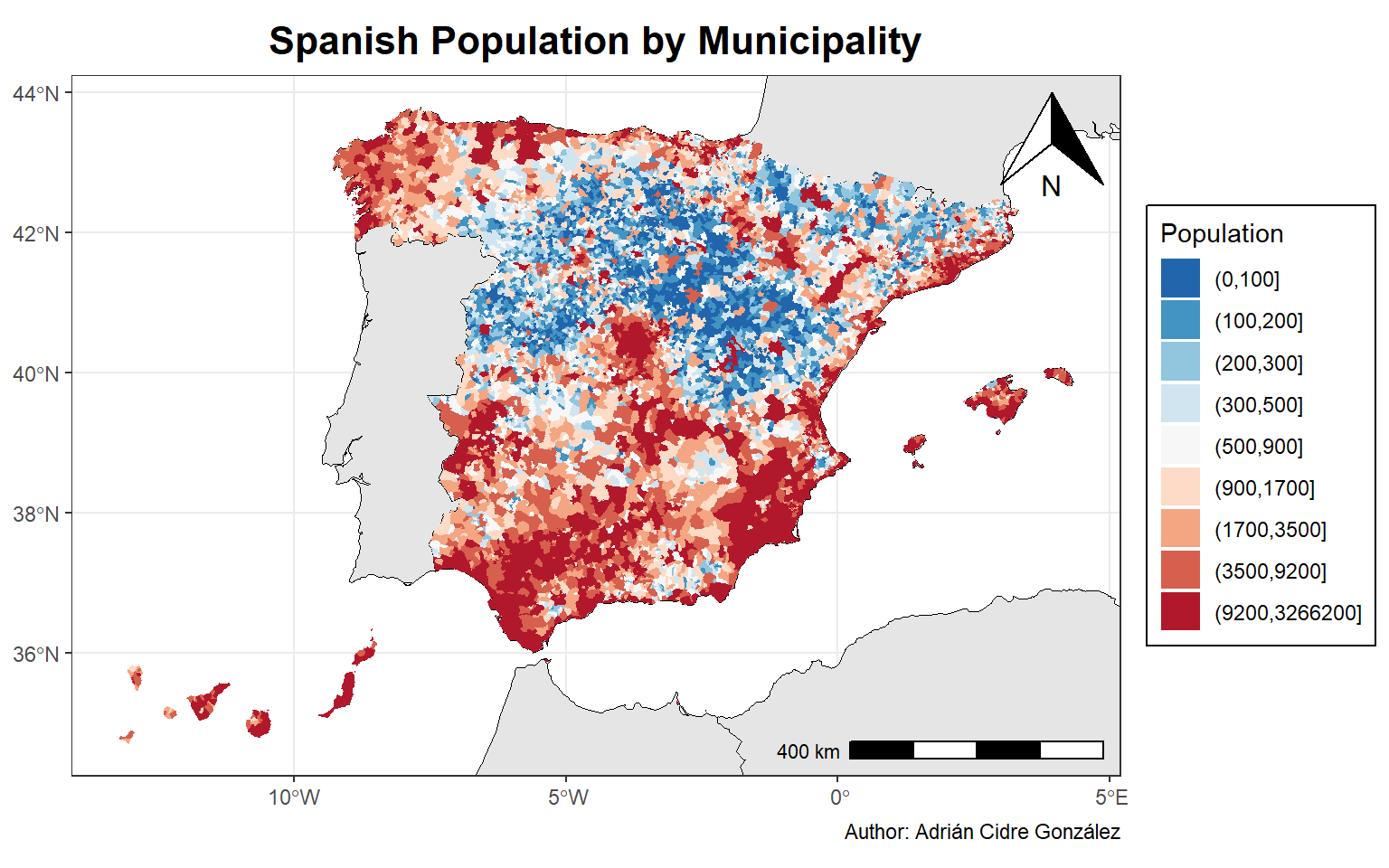
# Plot the population
ggplot(spain_pop_ready_sf) + 
  ## Geometries
  geom_sf(data = world_sf, fill = "grey90", color = "black") +
  geom_sf(aes(fill = pop_bin), color = NA) +
  ## Scales
  scale_fill_brewer(palette = "RdBu", na.translate = FALSE, direction = -1) +
  ## Labels
  labs(
    title   = "Spanish Population by Municipality",
    fill    = "Population",
    caption = "Author: Adrián Cidre González"
  ) +
  ## Coordinates
  coord_sf(xlim = st_bbox(spain_pop_ready_sf)[c(1,3)],
           ylim = st_bbox(spain_pop_ready_sf)[c(2,4)]) +
  ## Theme
  theme_bw() +
  theme(
    plot.title = element_text(hjust = 0.5, size = 16, face = "bold"),
    legend.background = element_rect(color = "black")
  ) +
  ## Ggspatial
  annotation_scale(location = "br") +
  annotation_north_arrow(location = "tr", which_north = "true")
Figure 2: Population in Spain by Municipality (2019)

We see some patterns in the distribution of the Spanish population. The central-north area exhibits a clear lower population than others areas., whereas coastal areas and islands area highly populated.

6 Ratio Men/Women

I will now create a similar visualization, but displaying the ratio between men and women by municipality. First, I create the new column:

# Ratio men-women
spain_pop_ready_sf <- spain_pop_sf %>% 
  mutate(ratio_mw = men/women)

summary(spain_pop_ready_sf$ratio_mw)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
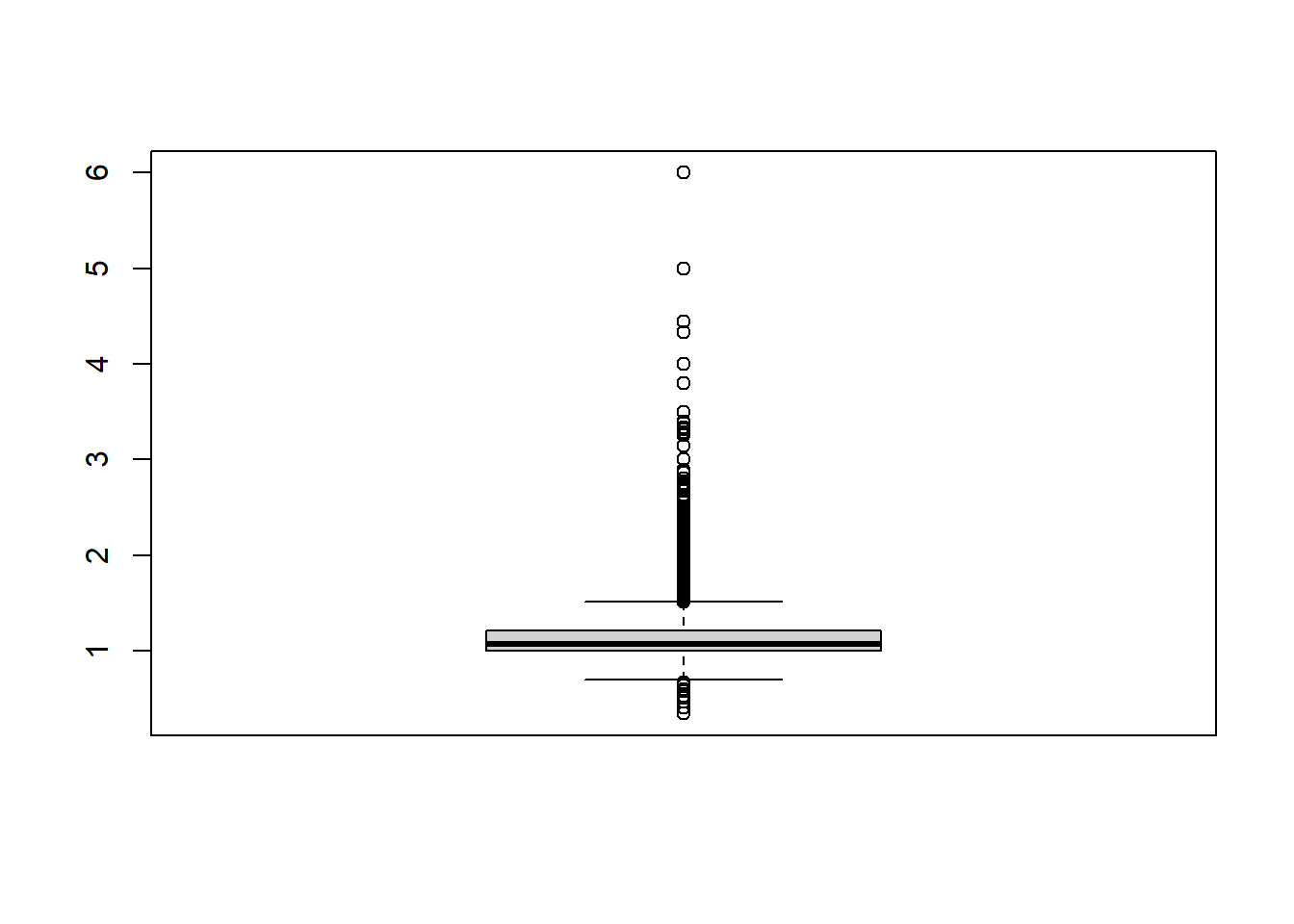
 0.3415  1.0003  1.0690     Inf  1.2067     Inf

We can see in the summary before that the values between the minimum and the \(3^{rd}\) quantile exhibit normal values, but the maximum value is infinite. This is because in some municipality there are men, but not woman (i.e. division by zero). We can see also the boxplot:

boxplot(spain_pop_ready_sf$ratio_mw)
Figure 3: Distribution of Men/Women ratio by municipallity

This tells us that a visualization of the continuous distribution will barely differentiate between area with higher women proportion (<1), and areas with higher men proportion (>1). Therefore, I apply the same approach creating bins:

# Define the breaks (bin edges) based on percentiles
breaks <- quantile(
  spain_pop_ready_sf$ratio_mw, 
  probs = seq(0, 1, by = 0.1)
)

# Round to hundred, and keep unique values
breaks <- round(breaks, 2) %>% unique()

# Create bins
spain_pop_ready_sf <- spain_pop_ready_sf %>% 
  mutate(
    ratio_bin = cut(ratio_mw, breaks = breaks)
  )

## Print bins
print(levels(spain_pop_ready_sf$ratio_bin))
 [1] "(0.34,0.96]" "(0.96,0.99]" "(0.99,1.01]" "(1.01,1.04]" "(1.04,1.07]"
 [6] "(1.07,1.11]" "(1.11,1.17]" "(1.17,1.26]" "(1.26,1.44]" "(1.44,Inf]"

With this code, a total of 10 bins are generated with the ranges showed above. So let’s proceed to the visualization:

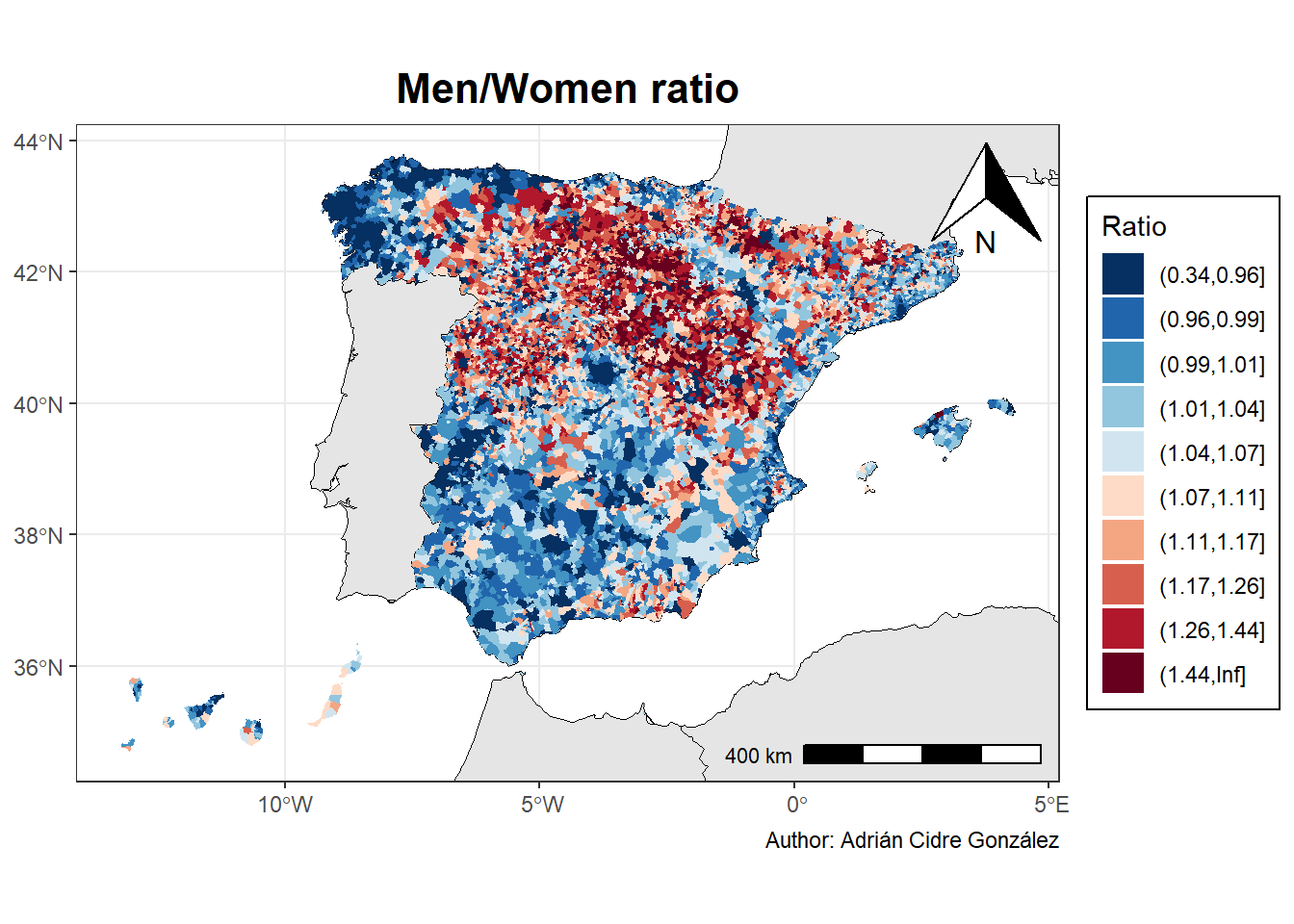
# Plot the population
ggplot(spain_pop_ready_sf) + 
  ## Geometries
  geom_sf(data = world_sf, fill = "grey90", color = "black") +
  geom_sf(aes(fill = ratio_bin), color = NA) +
  ## Scales
  scale_fill_brewer(palette = "RdBu", na.translate = FALSE, direction = -1) +
  ## Labels
  labs(
    title   = "Men/Women ratio",
    fill    = "Ratio",
    caption = "Author: Adrián Cidre González"
  ) +
  ## Coordinates
  coord_sf(xlim = st_bbox(spain_pop_ready_sf)[c(1,3)],
           ylim = st_bbox(spain_pop_ready_sf)[c(2,4)]) +
  ## Theme
  theme_bw() +
  theme(
    plot.title = element_text(hjust = 0.5, size = 16, face = "bold"),
    legend.background = element_rect(color = "black")
  ) +
  ## Ggspatial
  annotation_scale(location = "br") +
  annotation_north_arrow(location = "tr", which_north = "true")
Figure 4: Sex ratio in Spain by Municipality in 2019 (ratio men/women)

Curiously, we can see that the less populated areas are also populated mostly by men, whereas coastal areas and islands tend to be more balanced, or more populated by women.